CALDEIRÃO DE BOLSA

Jerok,

Muito Obrigado.
Acho que é uma leitura que qualquer Caldeirense deveria ter. Para quem não tem acesso ao trading directo de opções, penso que alguns produtos estruturados acabam por ser uma boa solução para esse tipo de investidores.

Obrigado pela tua fantástica contribuição e por teres esclarecido todas as minhas dúvidas

Conclusão:

A principal vantagem destes produtos, desde que de capital garantido, é o facto de beneficiar da evolução bolsista sem se
arriscar a perder dinheiro.

Ok, a YTM do produto é inferior à do mercado. Atendendo ao exemplo descrito, para uma valorização bolsista de 9000 para 12000 pontos
são cerca de 33,33% em três anos o que equivale um juro anual (yield to maturity) de 9,82%. O produto que criamos na melhor das hipóteses
dá 8,01%, mas não temos risco de mercado! (nota: existe sempre o risco do emitente, tal como num depósito a prazo).

Na pior das hipóteses, para o caso em concreto, recebemos 1% ao ano do valor investido. Não é muito, mas também não perdemos.

Não é necessário dominar a matemática da questão nem conhecer o mercado em detalhe. É importante ler a ficha técnica do
produto, ver se está confortável com risco do produto (se é de capital garantido, garante apenas uma percentagem do capital,
capital não garantido, etc...), verificar se as espectativas do produto coincidem com a sua visão da evolução do mercado, ou se
pelo contrário, pretende investir num produto que o compense da sua visão e eventuais outros investimentos que faça. Em qualquer
dos casos é importante apenas investir um montante do qual não necessite durante o perído do producto estruturado.

Esta sequencia de posts já vai longa, mas espero ter ajudado na compreensão de como o emitente constrói um produto estruturado,
no qual o cliente beneficia da valorização bolsista, sem que com isso o próprio emitente corra o risco de perder dinheiro.

(continuação)

Vamos supor, que construirmos este produto com um valor nominal de 1,000,000.00€ e
decidimos investir numa Call com valor de strike (St) igual a 9000.

Ou seja “apostamos” que o índice estará daqui a 3 anos com um valor superior a 9000 (um bull duradouro de 6 anos...).

Para determinarmos o numero de calls a comprar, é suficiente consultar a tabela anterior,
observando que o prémio de comprar um call de 9,000 é de 1,404€, e usar a seguinte fórmula:

#calls = (percentagem de Investimento) * (Valor Angariado dos Clientes) / (Prémio do Call)

usando os valores já obtidos até agora:

#calls = 10.88% * 1,000,000.00€ / 1,404€ = 77.5 calls

(como isto é meramente um exercício, irei considerar um valor decimal de contractos a comprar)

Somos agora felizes proprietários de 77.5 calls com strike de 9,000 pontos. Mas, daqui a 3 anos,
quanto valerá estas opções? E como se calcula o valor da opção, independentemente do valor
do Índice, daqui a 3 anos?

As fórmulas são simples:

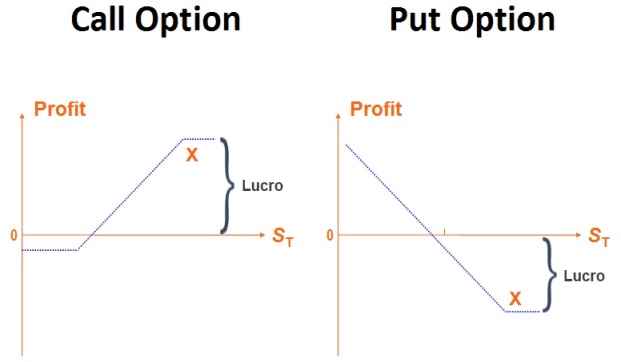
Lucro CALL = #calls * max(X – St, 0)

Lucro PUT = #calls * max(St - X, 0)

Relembro que como compramos calls com strike de 9000 => St = 9,000

Como é impossível neste momento saber como irá evoluir o índice durante um período tão vasto,
temos que traçar possíveis cenários, e determinar o valor a retribuir aos clientes.

1. Começamos com um cenário pessimista, em que X = 8000 ( ou qualquer valor inferir a 9000 )

Lucro = #calls * max(X – St, 0)

Lucro = 77.5 * max(8000 – 9000, 0)

Lucro = 77.5 * 0

Lucro = 0

Tendo em consideração que o cupão é de 1%, e como não ganhamos nada na componente variável,
neste caso obtemos uma yield to maturity (YTM) do produto estruturado de 1% (igual ao cupão, ou seja,
temos o capital garantido, que era um dos requisitos iniciais deste produto estruturado).


2. Num cenário mais favorável, em que St = 9500

Lucro = #calls * max(X – St, 0)

Lucro = 77.5 * max(9,500 – 9000, 0)

Lucro = 77.5 * 500

Lucro = 38,730€

Tendo em consideração que o cupão é de 1%, neste caso obtemos uma yield to maturity (YTM) do produto estruturado de 2,26%


3. Num cenário em que tínhamos acertado em cheio,e o valor do índice seja X = 12,000

Lucro = #calls * max(X – St, 0)

Lucro = 77.5 * max(12000 – 9000, 0)

Lucro = 77.5 * 3000

Lucro = 232,500€

Tendo em consideração que o cupão é de 1%, neste caso obtemos uma yield to maturity (YTM) do produto estruturado de 8,01%

(continua...)

(continuação)


Sob a perspectiva do emitente, o produto tem a seguinte estrutura de pagamentos:

no inicio do processo, investe todo o dinheiro obtido dos clientes;

no primeiro ano, paga o cupão de 1 %;

no segundo ano paga outro cupão de 1%;

e no final do produto, além do cupão de 1%, devolve o dinheiro investido e a Componente Variàvel (CV).

Para pagarmos o cupão do primeiro ano, iremos constituír um depósito a prazo,
que nos retorne a totalidade dos cupões a pagar.
Assim, depositamos a um ano, 1% do nosso capital, à taxa em vigor de 4,5%:

Deposito1Ano = 1% / (1+4,5%) ~= 0,96%

ou seja, depositamos 0,96% do nosso capital a um ano, e sabes com toda a certeza que nesse dia
iremos conseguir pagar os cupões aos clientes.

Se calculares quanto vale 0,96% do capital no dia de hoje, investido a uma taxa de 4,5% ao ano, obtemos 1%.
Ou seja, hoje precisamos menos que 1%, para ter 1% daqui a um ano.

Para o segundo ano, fazemos de forma idêntica:

Deposito2Ano = 1% / (1+4,7%)^2 ~= 0,91%

como usamos a capitalização contínua, e temos uma taxa no segundo ano mais elevada,
a percentagem do capital a investir é menor para garantir o mesmo valor de cupões.

Para o terceiro e último ano, não nos preocupamos agora com a Componente Variável (CV).
Neste momento pretendemos saber, qual o valor no nosso capital necessário para
liquidar na totalidade o produto.

Assim o valor necessário no último ano é:

Deposito3Ano = (1% + 100%) / (1+5%)^3 ~= 87,25%

Para determinarmos a totalidade a investir em depósitos a prazo, é suficiente realizar a seguinte soma:

TotalDeposito = Deposito1Ano + Deposito2Ano + Deposito3Ano

TotalDeposito = 0,96% + 0,91% + 87,25%

TotalDeposito = 89,12%

Desta forma, calculamos não apenas o valor a canalizar para depósito de capital garantido,
como também obtivemos o valor a ser investido no mercado financeiro:

Investimento = 100% - TotalDep

Investimento = 100% - 89,12%

Investimento = 10,88%

(continua...)

Vou tentar fornecer um exemplo bastante simples, de como criar um produto estruturado de raíz.
Apesar de ser um exemplo simples, envolve conceitos e fórmulas com as quais o leitor deve estar minimamente informado.

Eis o exemplo:

Vamos supor que uma instituição financeira, pretende comercializar um produto estruturado com os seguintes detalhes técnicos:

a) Valor garantido do capital investido

b) Tempo até à maturidade => 3 anos

c) Taxa fixa com cupão anual 1%

d) Taxa variável indexada à subida (se existir) do índice alemão DAX, daqui a 3 anos.

num cenário em que o mercado, vive um período saudável e tem taxas de retorno do activo sem risco, com a seguinte estrutura temporal:

1 ano => 4,5%

2 anos => 4,7%

3 anos => 5%

assumimos que o mercado de opções europeias sobre o DAX, negocia aos seguintes valores:



Um produto estruturado, na sua essência, é composto por:

A. uma componente em depósitos a prazo, que garantem a totalidade do capital investido

B. uma componente variável (com o valor que sobra da alínea anterior) para ser investido em opções.

Como se determina a percentagem a investir em depósitos?
E do que sobra, para investir em opções, como sabemos quantas devemos comprar?

(continua...)

K. Escreveu:O produto pode ser feito utilizando uma combinação de opções exóticas com depósitos a prazo (ou obrigações). Não é muito difícil de replicar, basta aplicar a variante da formula de Black-Scholes para estas opções.

Normalmente utilizam opções binárias tipo cash-or.nothing ou opções de barreira, que vão activando ou desactivando em valores pré-determinados.

http://en.wikipedia.org/wiki/Binary_option

Thank you! Para quem não tem acesso a essas opções exóticas acaba por ser vantajoso e prático comprar este tipo de produtos..
Vou dar uma olhadela na IB que já vi que eles têm coisas dessas e seminários sobre Opções.

O produto pode ser feito utilizando uma combinação de opções exóticas com depósitos a prazo (ou obrigações). Não é muito difícil de replicar, basta aplicar a variante da formula de Black-Scholes para estas opções.

Normalmente utilizam opções binárias tipo cash-or.nothing ou opções de barreira, que vão activando ou desactivando em valores pré-determinados.

http://en.wikipedia.org/wiki/Binary_option

Não, Muhamad. Eles "montam" esse género de estruturados e fazem a cobertura de risco, de forma a ganharem marginal mas seguramente. No fundo, um estrturado, não é nem mais nem menos do que uma série de produtos combinados, acrescidos de uma pequena margem para o Banco.

Um abraço,
Ulisses

canguru Escreveu:produto típico de final de bull...

Isso quer dizer que os bancos que comercializam este tipo de produtos podem estar sujeitos a perdas caso as acções continuem a valorizar?

ESAF NYSE Euronext Iberian ETF 19 Ago 14.440 1,002.29%


Não sei se este produto se pode emcaixar aqui.´

É possível ter um ganho de 1.000% este ano?


Pedro

Sr_SNiper Escreveu:

canguru Escreveu:produto típico de final de bull...

Não digas isso, ainda hoje o Tio Bem disse que o Bull é para continuar até à Lua

eu não digo nada, eu tento seguir tendências e ser disciplinado

mas não me apanham vinculados a produtos indexados à valorização de cabazes de ações até 2016

canguru Escreveu:produto típico de final de bull...

Yup, assim têm bonitas rentabilidades das acções do cabaz

canguru Escreveu:produto típico de final de bull...

Não digas isso, ainda hoje o Tio Bem disse que o Bull é para continuar até à Lua

produto típico de final de bull...

Sugiro a leitura a partir daqui.

Olá,

Queria saber um pouco o que acham deste tipo de produtos estruturados. O que não percebo muito é a forma como são criados.

Agora surgiu este novo Produtos Estruturado da Caixa Geral de Depósitos:

A Caixa Geral de Depósitos propõe até ao próximo dia 23 de Setembro o depósito indexado “Caixa Geral de Depósitos Acções Alemanha Setembro de 2016”, que deverá apenas ser equacionado por clientes sem risco de liquidez e com um montante mínimo de subscrição de mil euros. O período de investimento é de 3 anos, com reembolso previsto para 23 de Setembro de 2016.

Cumps
M.H.